平成30年春期試験問題 午前問43
問43解説へ
図のアローダイアグラムにおいて,プロジェクト全体の期間を短縮するために,作業A~Eの幾つかを1日ずつ短縮する。プロジェクト全体を2日短縮できる作業の組みはどれか。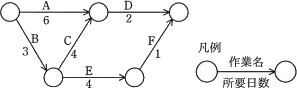

- A,C,E
- A,D
- B,C,E
- B,D
正解 エ問題へ
分野 :マネジメント系
中分類:プロジェクトマネジメント
小分類:タイムマネジメント
中分類:プロジェクトマネジメント
小分類:タイムマネジメント
広告
解説
まず図のアローダイアグラムにおけるクリティカルパスを求めます。以下、各作業を"作業名(作業日数)"で表記しています。
作業を短縮した後のクリティカルパスを選択肢ごとに再計算していきます。
- A(6) → D(2)=8日
- B(3) → C(4) → D(2)=9日
- B(3) → E(4) → F(1)=8日
作業を短縮した後のクリティカルパスを選択肢ごとに再計算していきます。
- A・C・Eを1日ずつ短縮すると、
A(5) → D(2)=7日
B(3) → C(3) → D(2)=8日
B(3) → E(3) → F(1)=7日
最短完了日数は8日で短縮可能日数は1日です。 - A・Dを1日ずつ短縮すると、
A(5) → D(1)=6日
B(3) → C(4) → D(1)=8日
B(3) → E(4) → F(1)=8日
最短完了日数は8日で短縮可能日数は1日です。 - B・C・Eを1日ずつ短縮すると、
A(6) → D(2)=8日
B(2) → C(3) → D(2)=7日
B(2) → E(3) → F(1)=6日
最短完了日数は8日で短縮可能日数は1日です。 - B・Dを1日ずつ短縮すると、
A(6) → D(1)=7日
B(2) → C(4) → D(1)=7日
B(2) → E(4) → F(1)=7日
最短完了日数は7日で短縮可能日数は2日です。
広告